Why does calibration target accuracy matter?

High-accuracy calibration targets ensure reliable camera testing, lens calibration, and optical quality control. Inaccurate targets can lead to measurement errors of 5-10% in MTF and distortion testing.

What are the quality grades for calibration targets?

Calibration targets are classified as high-precision (±0.01mm tolerance) for metrology labs, standard (±0.05mm) for general camera calibration, or general-purpose (±0.1mm) for educational applications.

What is Calibration
Target Accuracy?

Q: What is calibration target accuracy?

Calibration target accuracy refers to how precisely a test chart matches its designed specifications, including pattern precision, dimensional tolerance (typically ±0.01mm to ±0.1mm), substrate flatness, and contrast ratio uniformity.

When we talk about calibration target accuracy, we’re really asking one basic question: “How perfect is this pattern?” Just like when you buy a ruler, you want to make sure the measurements are correct. A calibration target works the same way – it needs to be extremely precise for your camera to work properly.

What is Feature Position Accuracy?

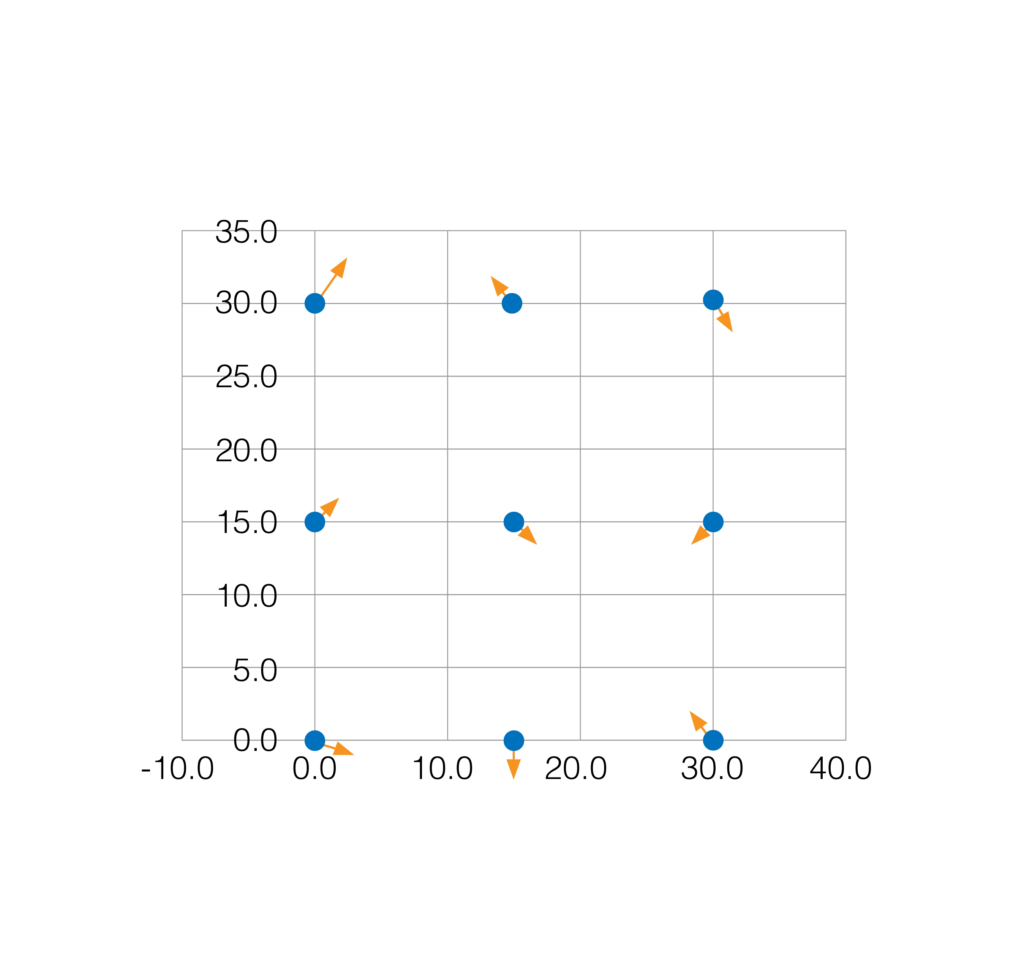
There are two main ways we check if a calibration target is accurate enough. The first is called feature position accuracy, which is basically asking “Are all the dots or squares in exactly the right spots?” Think of it like this: imagine you drew a perfect grid on a piece of paper with a computer, then tried to print it out. Position accuracy tells you how close your printed version is to that perfect computer drawing. If some dots ended up a little too far left or right, or up or down, that would show up as poor position accuracy.

What is Feature Spacing Accuracy?

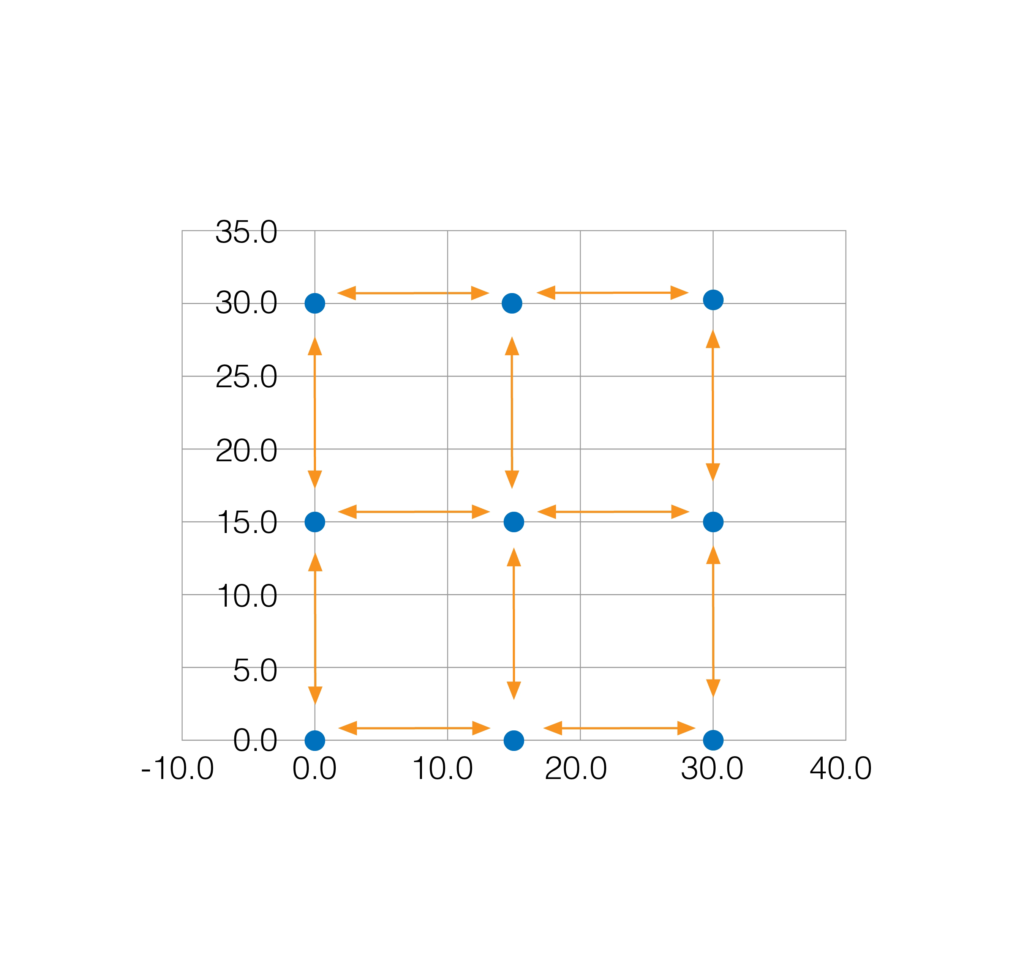
The second type is feature spacing accuracy, which asks a different question: “Are all the gaps between neighboring dots exactly the same size?” Picture a fence with evenly spaced posts. Even if each post is in roughly the right area, you’d still want the distance between post 1 and post 2 to be exactly the same as the distance between post 2 and post 3. That’s what spacing accuracy measures – the consistency of those gaps between features.

Why Calibration Target Accuracy Matters？

Both types of accuracy matter because they affect different things. If the overall positions are wrong, your entire measurement system will be shifted or twisted. If the spacing between features isn’t consistent, your measurements might be correct in some areas but wrong in others. It’s like having a ruler where the first few inches are accurate, but then the spacing gets gradually more compressed toward the end.

For anyone using machine vision or camera calibration systems, understanding these two accuracy types helps explain why some calibration targets cost more than others. A cheap target might look fine to your eyes, but when a computer tries to use it for precise measurements, those tiny position and spacing errors add up quickly. That’s why professional applications require targets with accuracy measured in microns – because even the smallest imperfections can throw off an entire measurement system.

Figure 1

Position Deviation Analysis

9-Point Grid Pattern (3×3 Array)

Figure 2

Position Deviation Analysis

12 Adjacent Feature Pairs

Feature Size Accuracy

Accuracy of dot diameter, square size, line width, and other feature dimensions

Minimum Feature Size

Smallest achievable feature size including minimum dot diameter, line width, and spacing resolution

Feature Spacing Accuracy

Accuracy of spacing between neighboring features including dot pitch, grid spacing, and line intervals

Feature Position Accuracy

Accuracy of feature positions relative to ideal coordinates across the entire pattern area

How to Measure Calibration Target Accuracy？

For most measurement results, the measured (x, y) positions may generally have an inclination or eccentricity effect regarding its ideal positions. The original (x, y) results are transformed by a best-fit 2D rigid transformation, which will not change relative position of all points, towards their ideal (x, y) value. After this transformation, the inclination and eccentricity effect of measured value can be eliminated.

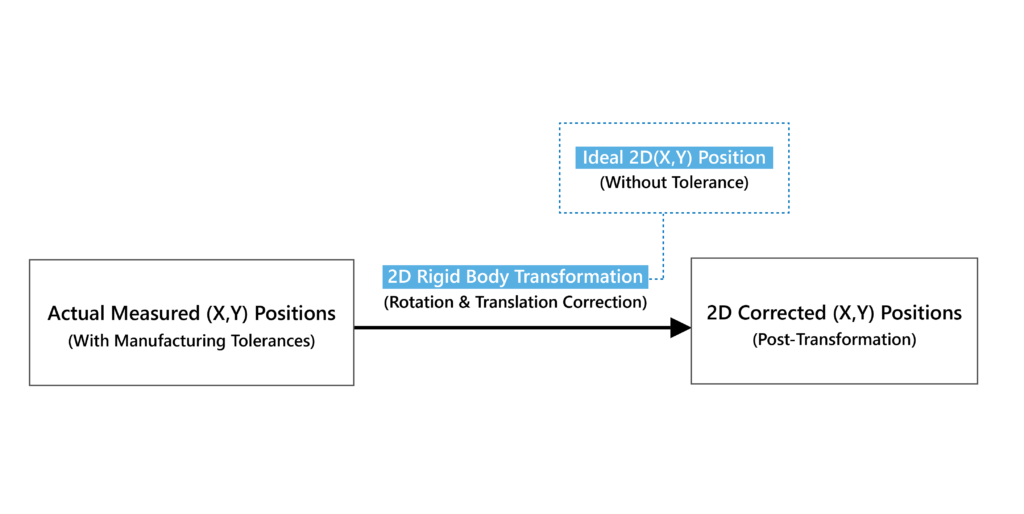
Actual Measured (X, Y) positions
Point Index	Actual X/mm	Actual Y/mm
1	-0.00069	0.00028
2	14.99929	0.00006
3	30.00429	0.00048
4	0.00106	14.99828
5	15.00132	14.99835
6	30.00636	14.99805
7	0.00280	29.99889
8	15.00330	29.99928
9	30.00874	29.99897

Ideal 2D (X, Y) Position
Point Index	Target X/mm	Target Y/mm
1	0	0
2	15	0
3	30	0
4	0	15
5	15	15
6	30	15
7	0	30
8	15	30
9	30	30

2D Affined (X, Y) Positions
Point Index	2D Rigid Transformed X/mm	2D Rigid Transformed Y/mm
1	-0.00264	0.00011
2	14.99734	0.00088
3	30.00234	0.00229
4	-0.00188	14.99811
5	14.99838	14.99917
6	30.00342	14.99986
7	-0.00113	29.99872
8	14.99937	30.00010
9	30.00481	30.00078

#01 Tolerance Analysis Example of

Feature Position Accuracy among Entire Pattern Area

For all 9 points, the positioning tolerance are calculated to know the tolerance distribution among the whole plate. And the maximum value of these tolerance will be Feature Position Accuracy among Entire Pattern Area. Here Point 9 (circled in red) has the maximum deviation from ideal positions, and the Feature Position Accuracy is 4.87μm.

Feature Position Accuracy among Entire Pattern Area
Point Index	Tolerances X/mm	Tolerances Y/mm	Distance vector of a point to its ideal (x, y) location
1	-0.00264	0.00011	0.00264
2	-0.00266	0.00088	0.00280
3	0.00234	0.00229	0.00327
4	-0.00188	-0.00189	0.00267
5	-0.00162	-0.00083	0.00182
6	0.00342	-0.00014	0.00342
7	-0.00113	-0.00128	0.00171
8	-0.00063	0.00010	0.00064
9	0.00481	0.00078	0.00487

#02 Tolerance Analysis Example of

Feature Spacing Accuracy of Any 2 Neighbor Points

There are totally 12 nearest-neighbor distances in 3 x 3 grid. Among these 12 distance values, the minimum and maximum value are -2.4um and +5.4um. It means, for the plate the Feature Spacing Accuracy of Any 2 Neighbor Points is [-2.4um, +5.4um].

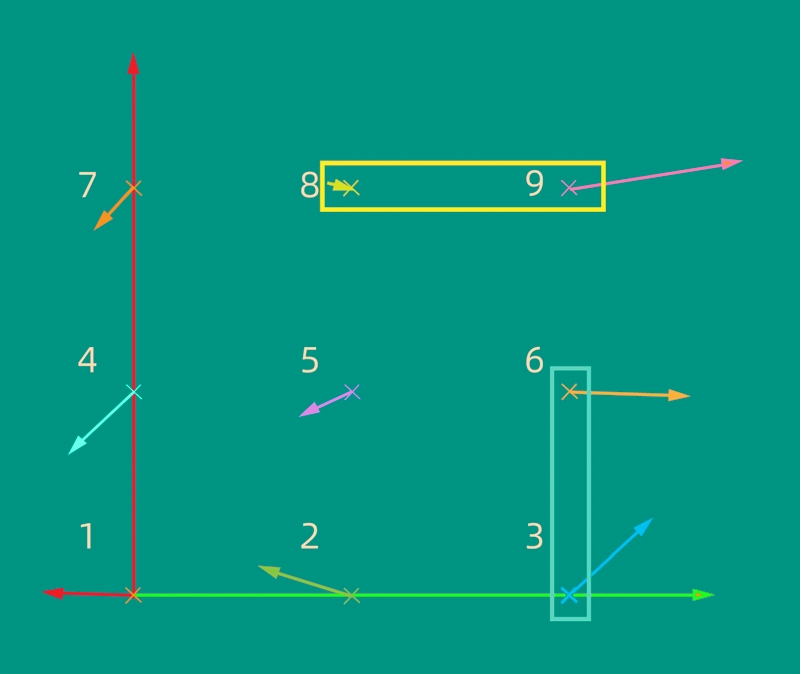
Feature Spacing Accuracy of Any 2 Neighbor Points (For 3 X 3 grid, there are 12 nearest-neighbor distances)
Distance Index	Distance	Actual 2-Point Distance Values	Ideal 2-Point Distance Values	Tolerance (Actual - Ideal)
1	Distance(1,2)	14.99998	15.00000	0.0000
2	Distance(1,4)	14.99800	15.00000	-0.0020
3	Distance(2,3)	15.00500	15.00000	0.0050
4	Distance(2,5)	14.99829	15.00000	-0.0017
5	Distance(3,6)	14.99757	15.00000	-0.0024
6	Distance(4,5)	15.00026	15.00000	0.0003
7	Distance(4,7)	15.00061	15.00000	0.0006
8	Distance(5,6)	15.00504	15.00000	0.0050
9	Distance(5,8)	15.00093	15.00000	0.0009
10	Distance(6,9)	15.00092	15.00000	0.0009
11	Distance(7,8)	15.00050	15.00000	0.0005
12	Distance(8,9)	15.00544	15.00000	0.0054

What is Calibration Target Accuracy?